Posts: 82
Threads: 5
Joined: Jul 2010
31 Jan 13, 02:34AM
(This post was last modified: 31 Jan 13, 02:51AM by ikljo.)
I have a hard math problem for everyone to try and figure out. It is very tricky, but after seeing #M|A#Wolf's thread, it appears as if we have a few math gods here. So maybe you might be able to figure it out. So here it goes...
The problem:
I've made 100 scripts which I've sold for exactly $100. I've sold python scripts for $5.00 each, javascripts for $2.00, and cube scripts for 10 cents.
How many of each type of script did I make?
Additional Details: I made a total of 100 scripts, no more, no less.
Anyone who solves this problem is a math god!
This problem can be solved
Posts: 2,841
Threads: 44
Joined: Jun 2010
Posts: 172
Threads: 5
Joined: Jun 2010
31 Jan 13, 02:58AM
(This post was last modified: 31 Jan 13, 03:00AM by GDM.)
70 cubescript, 19 javascript, 11 python scripts.
Wolf - the information you were missing was p >= 0, j >= 0, c >= 0
Posts: 2,144
Threads: 38
Joined: Aug 2010
31 Jan 13, 02:59AM
(This post was last modified: 31 Jan 13, 03:02AM by Oracle.)
11 Python Scripts, 19 Javascripts, 70 cubescripts.
Edit: Curses, GDM ;)
(HyPE helping HyPE xiters)
How to do it:
Say X=Python, Y=Java, Z=Cube
X + Y + Z = 100
5X + 2Y + 0.1Z = 100
X, Y, Z must be whole numbers
Z has to be a multiple of 10, since the other two will give only whole numbers (5x, 2y)
So I started from top to bottom, plugging in values of Z - can't be 100, 90, 80
Plug in 70
X + Y = 30
5X + 2Y = 93
Multiply the first equation by -2
3X = 33
X = 11, plugging in X in either one gives Y = 19
Hence 11, 19, 70
Posts: 82
Threads: 5
Joined: Jul 2010
31 Jan 13, 03:43AM
(This post was last modified: 31 Jan 13, 03:54AM by ikljo.)
Set up your equations:
P = # of python scripts
J = # of javascripts
C = # of Cubescripts
P + J + C = 100
5P + 2J + C/10 = 100
multiply the 2nd equation by 10 and subtract the two equations from each other
10(5P + 2J + C/10 = 100)
=> 50P +20J + 10C/10 = 1000
Subtract: P + J + C = 100
==> 49P + 19J = 900
Now, there are lots of ways to do that, but you need both P and J to be integers. Notice that 900 is divisible by 10. Divide the whole equation by 10
$4.9 P + $1.9 J = $90
Now, you know that I need to make exactly $90 selling just python scripts and javascripts. Each time I sell a script, I have to give a dime in change. To get back to an exact dollar figure, I will need to sell some multiple of 10 scripts. So, make the substitution
P + J = 10 n
Now, solve for P and substitute
49 n - 3 J = 90
Remembering that n and J are both integers, n must be a multiple of 3 (divide that equation by 3 and see). So try, n=3, 6, 9, etc.
For n=3, J = 19
For n=6, J = 68
For n=9, J = 117 (which is impossible.)
If J = 19, then P = 11 and C = 70.
If J = 68, then P = -8 which is impossible.
So, the only possible answer is 11 python scripts, 19 javascripts and 70 cubescripts.
Posts: 86
Threads: 6
Joined: Jun 2010
Posts: 2,067
Threads: 11
Joined: Jun 2010
(31 Jan 13, 07:44AM)Takkunen Wrote: ... Window.
Posts: 534
Threads: 10
Joined: Oct 2010
1. Ben and Shaun each put $20 into a bag.
2. Shaun then "buys" the bag with the money in it for $30 from Ben.
3. ????
4. Profit?
Posts: 1,718
Threads: 169
Joined: Jun 2010
31 Jan 13, 11:50AM
(This post was last modified: 31 Jan 13, 11:55AM by MykeGregory.)
(31 Jan 13, 10:21AM)Fate Wrote: 1. Ben and Shaun each put $20 into a bag.
2. Shaun then "buys" the bag with the money in it for $30 from Ben.
3. ????
4. Profit? Profit? Yes! Both parties receive $10 profit. BOOM!
http://forum.cubers.net/thread-2305.html
Posts: 92
Threads: 8
Joined: Jun 2010
Huehuehue
![[Image: xminusshit.png]](http://img822.imageshack.us/img822/7140/xminusshit.png)
Posts: 2,841
Threads: 44
Joined: Jun 2010
Posts: 534
Threads: 10
Joined: Oct 2010
01 Feb 13, 08:24AM
(This post was last modified: 01 Feb 13, 08:24AM by Fate.)
(31 Jan 13, 11:50AM)MykeGregory Wrote: (31 Jan 13, 10:21AM)Fate Wrote: 1. Ben and Shaun each put $20 into a bag.
2. Shaun then "buys" the bag with the money in it for $30 from Ben.
3. ????
4. Profit? Profit? Yes! Both parties receive $10 profit. BOOM!
http://forum.cubers.net/thread-2305.html
(╯°□°)╯︵ ┻━┻
Posts: 1,718
Threads: 169
Joined: Jun 2010
(01 Feb 13, 08:24AM)Fate Wrote: (╯°□°)╯︵ ┻━┻
^^ Indeed.
Posts: 308
Threads: 12
Joined: Aug 2010
01 Feb 13, 02:55PM
(This post was last modified: 01 Feb 13, 02:56PM by Aekom.)
(31 Jan 13, 02:38PM)PolarHedgehog Wrote: Huehuehue
![[Image: xminusshit.png]](http://img822.imageshack.us/img822/7140/xminusshit.png)
That's x-3/x-1 when finding common factors.
Posts: 2,841
Threads: 44
Joined: Jun 2010
(01 Feb 13, 02:55PM)Aekom Wrote: (31 Jan 13, 02:38PM)PolarHedgehog Wrote: Huehuehue
![[Image: xminusshit.png]](http://img822.imageshack.us/img822/7140/xminusshit.png)
That's x-3/x-1 when finding common factors. The answer's 1.
Posts: 2,144
Threads: 38
Joined: Aug 2010
^Nope, Aekom is indeed correct.
Posts: 92
Threads: 8
Joined: Jun 2010
02 Feb 13, 06:14AM
(This post was last modified: 02 Feb 13, 06:14AM by PolarHedgehog.)
Quote:Party A received 36% of the votes in the first elections. The voting percentage was 85%. In the second elections, party A received 38% of the votes, and the voting percentage was 80%. How many percent more or less votes did party A get in the second elections than in the first? The number of voters did not change between the elections.
ps 9th grade ftw.
Posts: 971
Threads: 81
Joined: Dec 2010
lol----
Want to find out how many steps are visible in an escalator. To this was done the following: two people began climbing an escalator together, one going one step at a time while the other climbed two . On top the first person counted 21 steps while the other 28. With this data it was possible to answer the question. How many steps are visible on that escalator? (Note: escalator is operating).
[/u]
Posts: 172
Threads: 5
Joined: Jun 2010
(02 Feb 13, 06:43AM)1Cap Wrote: lol----
Want to find out how many steps are visible in an escalator. To this was done the following: two people began climbing an escalator together, one going one step at a time while the other climbed two . On top the first person counted 21 steps while the other 28. With this data it was possible to answer the question. How many steps are visible on that escalator? (Note: escalator is operating).
[/u]
The person who was skipping every other step took more total steps than the person who wasn't? Were they going up a down escalator?
Posts: 93
Threads: 2
Joined: Jun 2010
k here's an easy question .
How many different nine digit numbers can be formed from the number 223355888 by rearranging its digits so that odd digits occupy even position ?
Posts: 2,144
Threads: 38
Joined: Aug 2010
I think I did this wrong (I kinda forget the permutations/combinations w/ repeats) but...
(5! x 4!)/(2! x 2! x 2! x 3!) = 60 numbers?
Posts: 93
Threads: 2
Joined: Jun 2010
04 Feb 13, 05:22AM
(This post was last modified: 04 Feb 13, 06:56AM by Flames.)
yep
One more question :
Let ABC be a triangle such that angle ACB = Pi/6 [ :D no idea how to insert the image] and let a,b and c denote the lengths of the sides opposite to A,B and C respectively. The value of x for which a= x^2+x+1,b=x^2-1 and c=2x+1 is ..
Posts: 2,144
Threads: 38
Joined: Aug 2010
(04 Feb 13, 05:22AM)Flames Wrote: The value of x for which a= x^2+x+1=x^2-1 and c=2x+1 is .. Was there supposed to be a "b=x^2-1"?
Posts: 93
Threads: 2
Joined: Jun 2010
(04 Feb 13, 06:32AM)ShadowFlameZ Wrote: (04 Feb 13, 05:22AM)Flames Wrote: The value of x for which a= x^2+x+1=x^2-1 and c=2x+1 is .. Was there supposed to be a "b=x^2-1"? Oops fixed now
Posts: 799
Threads: 52
Joined: Jan 2011
04 Feb 13, 01:02PM
(This post was last modified: 04 Feb 13, 01:02PM by Roflcopter.)
(04 Feb 13, 05:22AM)Flames Wrote: Let ABC be a triangle such that angle ACB = Pi/6 [ :D no idea how to insert the image] and let a,b and c denote the lengths of the sides opposite to A,B and C respectively. The value of x for which a= x^2+x+1,b=x^2-1 and c=2x+1 is ..
Hint: use the cosine law rearranged into cos C = (a^2+b^2-c^2)/(2ab). We know angle C and we know a, b and c. This will give us a quadratic equation in R[x] with only one viable root (the other is negative).
Posts: 172
Threads: 5
Joined: Jun 2010
04 Feb 13, 09:17PM
(This post was last modified: 04 Feb 13, 09:19PM by GDM.)
(04 Feb 13, 01:02PM)Roflcopter Wrote: (04 Feb 13, 05:22AM)Flames Wrote: Let ABC be a triangle such that angle ACB = Pi/6 [ :D no idea how to insert the image] and let a,b and c denote the lengths of the sides opposite to A,B and C respectively. The value of x for which a= x^2+x+1,b=x^2-1 and c=2x+1 is ..
Hint: use the cosine law rearranged into cos C = (a^2+b^2-c^2)/(2ab). We know angle C and we know a, b and c. This will give us a quadratic equation in R[x] with only one viable root (the other is negative).
Yeah. No one is bothering because this isn't a "really hard" or even "hard" math problem. It's an obvious use of a common formula.
Also: plugged into wolfram
Posts: 799
Threads: 52
Joined: Jan 2011
What are the last 10 digits of tet(2337, 2339)?
You're given that tet(a,0) = 1 and that tet(a,b+1) = a^tet(a,b) for a and b non-negative integers.
See Wikipedia on tetration.
Posts: 2,230
Threads: 32
Joined: Jun 2011
the answer always is:
![[Image: Pi-CM.svg]](https://upload.wikimedia.org/wikipedia/commons/f/f3/Pi-CM.svg)
Posts: 308
Threads: 12
Joined: Aug 2010
05 Feb 13, 10:23PM
(This post was last modified: 05 Feb 13, 10:26PM by Aekom.)
(05 Feb 13, 01:28PM)Roflcopter Wrote: What are the last 10 digits of tet(2337, 2339)?
You're given that tet(a,0) = 1 and that tet(a,b+1) = a^tet(a,b) for a and b non-negative integers.
See Wikipedia on tetration.
I'm not going to pretend I know anything about Tetration, but I thought I'd have a go anyway. As far as I understand, Tetration is iterated powers (powers of a power). I'm assuming that tet(a,0) = 1 is another notation style for ![[Image: 6wExGYL.png]](http://imgur.com/6wExGYL.png) (please correct me if I'm just making stuff up here).
I tried to give it a go through WolframAlpha using the information from this thread:
http://community.wolframalpha.com/viewto...20&t=73980
and it came back with "indeterminate": http://www.wolframalpha.com/input/?i=+Po...2C+{2339}]
Posts: 2,387
Threads: 56
Joined: Aug 2010
(31 Jan 13, 11:50AM)MykeGregory Wrote: (31 Jan 13, 10:21AM)Fate Wrote: 1. Ben and Shaun each put $20 into a bag.
2. Shaun then "buys" the bag with the money in it for $30 from Ben.
3. ????
4. Profit? Profit? Yes! Both parties receive $10 profit. BOOM!
http://forum.cubers.net/thread-2305.html
SCAM
|



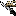
![[Image: xminusshit.png]](http://img822.imageshack.us/img822/7140/xminusshit.png)
![[Image: 6wExGYL.png]](http://imgur.com/6wExGYL.png) (please correct me if I'm just making stuff up here).
(please correct me if I'm just making stuff up here).